domingo, 7 de octubre de 2018
viernes, 10 de agosto de 2018
martes, 31 de julio de 2018
PUNTO MEDIO DE UN SEGMENTO
Las coordenadas del punto medio de un segmento coinciden con la semisuma de las coordenadas delos puntos extremos.
EJEMPLO:
Hallar las coordenadas del punto medio del segmento AB.
También puede darse el caso de que se conozca un extremo
y el PM (punto medio). De ser así se debe realizar el siguiente
procedimiento:
EJERCICIOS: ENCUENTRE EL PUNTO MEDIO DE LOS SIGUIENTES SEGMENTOS DE RECTA. GRAFIQUE CADA EJERCICIO:
1.- (8,3) (20,10)
2.- (2,4) (-10,-3)
3.- (-5,-6) (-1,-1)
4.- (4,9) (-10, -3)
5.- (-1,-2) (-12,-10)
6.- (-8,3) (5,10)
7.- (8,-3) (2,-10)
8.- (-8,-3) (-2,-10)
EJERCICIOS: ENCUENTRE LA CORDENADA DEL EXTREMO FALTANTE DE LOS SIGUIENTES SEGMENTOS DE RECTA. GRAFIQUE CADA EJERCICIO:
1.- PM(2,3) A(2,10)
2.- PM(2,2) T(-10,-3)
3.- PM(-5,-2) P(-1,-1)
4.- PM(4,1) Q(-2, -3)
5.- PM(-1,-2) Z(-7,-3)
6.- PM(-2,3) S(5,1)
7.- PM(3,-3) W(2,-3)
8.- PM(-2,-3) R(-2,-2)
EJERCICIOS DE PERIMETROS Y AREAS
INSTRUCCIONES: Obtenga el área y el perímetro de cada una de las siguientes figuras.
AREA DE FIGURAS EN EL PLANO
NOTA: Para las figuras de mas de tres lados, se puede proceder dividiéndola en varios triángulos, cuadrados o rectángulos para calcular las áreas y sumarlas al ultimo para poder conocer el área final.
EJERCICIO:
La siguiente figura se dividió en dos triángulos para poder obtener su área. Utilizando la formula del ejemplo, obtenga el área resultante.
DISTANCIA ENTRE DOS PUNTOS
Por haberlo estudiado, sabemos que el
Plano cartesiano
se usa como un sistema de referencia para localizar puntos en un plano.
Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje
x
(de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas
(x
2
– x
1
) y de manera igual para el eje Y en caso de estar sobre este eje.
Ejemplo:
La distancia entre los puntos (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje
y
(de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Para demostrar esta relación se deben ubicar los puntos
P
1
(x
1
, y
1
)
y
P
2
(x
2
, y
2
)
en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa
P
1
P
2
y emplear el
Teorema de Pitágoras
.
INTRODUCCION AL BLOQUE 1
GEOMETRIA.
La geometría (del latín geometrĭa, y este del griego γεωμετρία de γῆ gē, ‘tierra’, y μετρία metría, ‘medida’) es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, superficies, curvas, etc.
PLANO CARTESIANO.
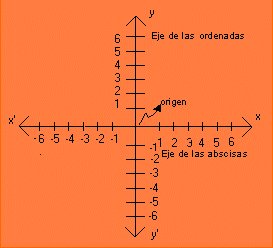
El plano cartesiano está formado por dos rectas
numéricas, una horizontal y otra vertical que se cortan en
un punto. La recta horizontal es llamada eje de las abscisas o de
las equis (x), y la vertical, eje de las ordenadas o de las yes,
(y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la
posición de puntos, los cuales se representan por sus
coordenadas o pares ordenados. Las coordenadas se forman
asociando un valor del eje
de las "X" y uno de las "Y", respectivamente, esto indica que un
punto se puede ubicar en el plano cartesiano con base en sus
coordenadas, lo cual se representa como:
P (x,
y)
Para localizar puntos en el plano cartesiano se debe
llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan
las unidades correspondientes hacia la derecha si son positivas o
hacia a izquierda si son negativas, a partir del punto de origen,
en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan
las unidades correspondientes hacia arriba si son positivas o
hacia abajo, si son negativas y de esta forma se localiza
cualquier punto dadas sus coordenadas.
Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este
procedimiento también se emplea cuando se requiere
determinar las coordenadas de cualquier punto que esté en
el plano cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).
De lo anterior se concluye que:
Para determinar las coordenadas de un punto o localizarlo en
el plano cartesiano, se encuentran unidades correspondientes en
el eje de las x hacia la derecha o hacia la izquierda y luego las
unidades del eje de las y hacia arriba o hacia abajo,
según sean positivas o negativas, respectivamente.
Doña Lupe nos ha dicho que su
farmacia está dentro del centro de la ciudad .
Supongamos que deseamos saber la ubicación exacta de
la farmacia de Doña Lupe Una vez que ya
estamos en el centro le preguntamos a un
policía para que nos oriente. El policía nos ha
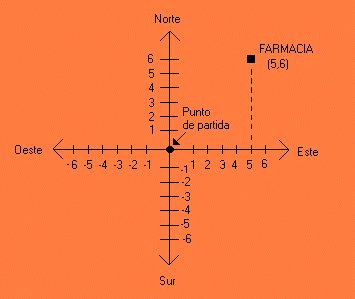
dicho que caminemos 5 cuadras hacía el este y 6 cuadras
hacía el norte para llegar a la farmacia. La cantidad de
cuadras que tenemos que caminar las podemos entender como
coordenadas en un plano cartesiano.
Lo anterior lo podemos expresar en un plano cartesiano de la
siguiente manera:
Para el problema planteado , el origen del plano será
el punto de partida que es en donde le preguntamos al
policía sobre la ubicación de la farmacia.
ACTIVIDAD.
INSTRUCCIONES:
LOCALIZA LAS SIGUIENTES COORDENADAS EN UN PLANO CARTESIANO.
EN EL PRIMER PLANO: (3 ,0) (6 ,0) (6 ,1) (7 ,1) (8 ,2) (8
,4) (9 ,4) (8 ,6) (10 ,7) (1,7) (1,9)
(7 ,9) (8 ,7). ( 1,7 ) (1 ,4 ) (2 ,3 ) (2 ,4 ) (3 ,4 ) (3
,6 ) (4 ,6 ) (4 ,5 ) (5 ,5 ) (5 ,7 ).
(6 ,7) (8 ,6). (7,3) (8
,3). (3 ,4) (4 ,3). (6, 5) (7, 5) (7 ,6) (6 ,5). (2 ,4) (3 ,1) (3 ,0).
EN EL SEGUNDO PLANO: (5 ,1 ) (7 ,1 ) (9 ,3 ) (9 ,5 ) ( 7,
7) (5 ,7 ) (3 ,5 ) (3 ,3 ) (5,1).
(7 ,5) (10, 9) (8,11) (6 ,11) (4 ,9) (10,9).
(7 ,5) (8 ,5). (7 ,5) (4 ,6).
EN EL TERCER PLANO:
Suscribirse a:
Entradas (Atom)